Die mittlere aerodynamische FLÜGELTIEFE t_m

     Ohne Bestimmung der mittleren aerodynamische Flügeltiefe t_m ist in den meisten Fällen die genaue Schwerpunktbestimmung kaum möglich. In diesem Beitrag wird vor allem neben der formelmäßigen, auch die zeichnerische Ermittlung an Hand einiger geometrischer Beispiele besprochen.

       Einleitend sei gesagt: um ein bisschen mathematisches Grundwissen, mit dem Teilbereich Geometrie, kommt man bei der Bewältigung dieser Aufgabe nicht herum. Ein einfacher Taschenrechner und eine Formeltabelle aus einem Taschenkalender sollten jedoch für die Flächenberechnung der gängigsten Flügelgrundrisse genügen. Zum zeichnen unsymmetrischer Grundrisse im Maßstab 1 : 10 ist Millimeterpapier hilfreich.

Was genau ist nun eigentlich diese mittlere aerodynamische Flügeltiefe t_m und wozu dient sie? Die für ein Flugmodell in Prozent oder Millimeter angegebene Schwerpunktrücklage steht immer in Bezug zu t_m. Da t_m aber häufig nicht mit der Größe und Lage des Wurzelprofils übereinstimmt, ist ihre Bestimmung unumgänglich. Ihre Größe (m) kann immer rechnerisch, ihre Lage (m) aber in vielen Fällen nur zeichnerisch erfasst werden.
       Bei einem Rechteckflügel ist die geometrische Flügeltiefe auch gleichzeitig die mittlere aerodynamische Flügeltiefe (Abb: 1). Sie entspricht der Flügeltiefe des Wurzel- und Endprofils, also jedes x-beliebigen.

      Bei einem Tragflügel, der keinen rechteckigen Grundriss aufweist, ist die mittlere aerodynamische Flügeltiefe die Tiefe eines gedachten Rechteckflügels, der bei gleicher Flügelfläche und bei gleichem Anstellwinkel wie der gegebene Flügel die gleiche Gesamtluftkraft nach Größe und Richtung wie dieser liefert (Abb:2). Hier unterscheidet sich t_m wesentlich in Größe und Lage von und zu den unterschiedlichen geometrischen Flügeltiefen.

Die Zauberformel zur rechnerischen Bestimmung von t_m aller Grundrisse lautet: t_m = F / b. Darin ist F die Flügelfläche (Flächeninhalt des Grundrisses) und b die Spannweite. Egal welche Form der Flügelgrundriss auch hat, für die Spannweite b gilt immer die Entfernung, gemessen in einem rechten Winkel, von der Wurzel- zur Endrippe! Wohl gibt das Formelergebnis prompt die Profiltiefe von t_m an, leider aber nicht in allen Fällen auch ihre Lage. Diese Bestimmung entpuppt sich zuweilen als der weit schwierigere Teil und kann dann nur auf geometrischem Weg gefunden werden.

Bei den folgenden, exemplarischen Rechenbeispielen und erläuternden Zeichnungen wird für b nur die Halbspannweite und daher auch nur der halbe Flächeninhalt der Tragfläche eingesetzt.
       Achtung: bei allen symmetrischen Flügelgrundrissen, egal ob Trapez, gleichseitiges Dreieck, Ellipse oder sonstige Grundrissformen kann die errechnete mittlere Flügeltiefe t_m sofort in das Mittel der Wurzelrippe übertragen werden! (die Mittellinie aller Flächenteile muss senkrecht zur Wurzelrippe stehen und die so halbierten Flächenteile kongruent sein).

Als Beispiel: eine Rechteckfläche mit einem elliptischen Ohr (Abb:3). Die Halbspannweite setzt sich aus 0,6 m für den Rechteckteil und 0,3 m für die Halbellipse zusammen = 0,9 m. Die Wurzeltiefe beträgt 0,18m. Das ergibt für den Rechteckteil der Tragfläche 0,18 * 0,6 = 0,108 m² und für die Halbellipse (0,09 * 0,3 * π [pi]) /2 = 0,0424 m², zusammen ist F = 0,1504 m² und t_m = 0,1504 / 0,9 = 0,167 m. Da nun die durch eine senkrecht zur Wurzelrippe stehende und fortlaufend gerade Mittellinie entstandenen Grundrisshälften deckungsgleich sind, kann t_m von 0,167 gleich mittig in das Wurzelprofil übertragen werden. In Zeichnung 4 ist ein einfacher Flächengrundriss dargestellt, bei dem die Mittellinie nicht senkrecht zur Wurzelrippe steht. Zuerst errechnet man den Flächeninhalt. Die Abmessungen sind: Halbspannweite 0,9 m, Wurzelrippe 0,25 und Endrippe 0,2 m. F = (0,25 + 0,2)/2 * 0,9 = 0,2025 m². Nach obiger Formel ist daher t_m = 0,2025 / 0,9 = 0,225 m.

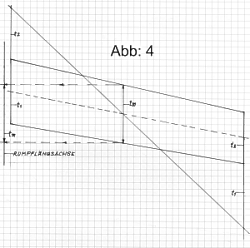Aus Abbildung 4 ist jetzt auch ein geometrische Weg ersichtlich, wie man die richtige Lage von t_m findet. Zuerst wird eine Grundrissmittellinie eingezeichnet. Das ist die Verbindungslinie von den Mittelpunkten des Wurzel- und Endprofils. Senkrecht zur und oberhalb der Wurzelrippe wird die Länge der Endrippe aufgetragen und unterhalb der Endrippe, die Länge der Wurzelrippe. Ihre Endpunkte werden mittels Diagonallinie verbunden und dort, wo diese die Mittellinie schneidet, befindet sich senkrecht zum Koordinatensystem die aerodynamische Flügeltiefe t_m. Wurde richtig gerechnet, ist ihre Länge 0,225 m. Falls nicht, lässt sich anhand der Formel F = t_m * b der Flächeninhaltwert überprüfen. Mit Hilfe eines rechtwinkeligen Dreiecks wird die Tiefe von t_m nun in die Wurzelrippe übertragen und so die richtige Lage für t_m gefunden.

Wäre nun zu letztem Beispiel der Schwerpunkt x_S mit 40% angegeben, so liegt er bei 0,2025 * 0,4 = 0,081 m oder 81 mm, gemessen von der Nase von t_m. Ist er mit 81 mm angegeben, dann lautet die Rechnung (0,081 / 0,2025) * 100 = 40%. Vorsichtshalber sei noch einmal erwähnt: diese 81 mm gelten für t_m und nicht für die Wurzelrippe! Daher ist es immer wichtig, nach der Lagefindung von t_m, diese exakt auf die Rumpfseitenfläche unterhalb der Tragfläche zu übertragen!

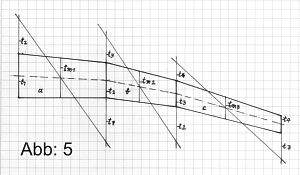Die Abbildung 5 zeigt als letztes Beispiel einen komplizierteren Grundriss, bestehend aus drei verschiedenen Teilabschnitten. Die Halbspannweite beträgt 1,5 m mit den Teillängen a - c gleich 0,5 m, 0,4 m, und 0,6 m. Die geometrischen Profiltiefen t₁ - t₄ betragen von der Wurzel beginnend: 0,25 m, 0,2 m, 0,15 m und 0,1 m. Wie nach obigen Beispiel errechnet, beträgt der Flächeninhalt der Teilabschnitte a = 0,1125 m², b= 0,7 m² und c = 0,75 m², zusammen also 0,2575 m². Nach der schon geläufigen Formel ist demnach t_m = 0,2575 / 1,5 = 0,1716 m. Auch die nun erforderlichen Mittellinien werden wie vorherbeschrieben eingezeichnet und auch für jedes Teiltrapez mittels Diagonallinie die mittlere Flügeltiefe für a, b und c gefunden. Verbindet man die Endpunkte der neu gefundenen Profiltiefen t_m1 - t_m2 und t_m2 - t_m3, erhält man zwei neue Trapeze (Abb: 6). Nun muß wie vorher die dazu passende mittlere Flügeltiefe gesucht werden, also neue Mittellinie einzeichnen und dann wie gelernt die Diagonallinie ziehen. Aus den zwei neuen Profiltiefen t_m4 und t_m5 entsteht nun das letzte entscheidende Trapez (Abb: 7). Die nach der gleichen Methode gefundene mittlere Tiefe ist schließlich die lang gesuchte mittlere Flügeltiefe t_mF der gesamten Tragfläche. Wird sie zur Wurzelrippe parallel verschoben, erkennt man überrascht, wie weit sie von dieser zurückversetzt liegt.

In diesem Beitrag wurde für den ambitionierteren, an Flugmechanik interessierten Modellflieger anhand einiger ausgesuchter Beispiele die Größen- und Lagefindung der mittleren Flügeltiefe t_m formelmäßig und zeichnerisch behandelt und versucht, ihre Wichtigkeit bei der Lokalisierung des Schwerpunktes x_s hervorzuheben. Darüber hinaus soll diese Arbeit für den in der nächsten 'prop'-Folge erscheinenden Beitrag, 'Die vertrackte Schwerpunktbestimmung', eine Hilfestellung geben.



Abbildung 1: beim Rechteck ist die geometrische Flügeltiefe t_m gleich der aerodynamischen t_m.
Abbildung2: Wurzel- und Endprofil der Trapezfläche, als geometrische Flügeltiefen, unterscheiden sich von der aerodynamischen Flügeltiefe t_m.
Abbildung 3: bei allen Grundrissen deren Grundrisshälften deckungsgleich sind und deren Mittellinie fortlaufend gerade verläuft und senkrecht zur Wurzelrippe steht, kann die errechnete t_m gleich mittig in das Wurzelprofil übertragen werden.
Abbildung 4: zeigt den geometrischen Weg zur Findung von t_m.
Abbildung 5, 6 und 7 zeigen die schrittweise geometrische Lösung für t_m bei einem komplizierteren Grundriss mit Teilflächen, bei denen weder die Mittellinie geradlinig verläuft noch senkrecht zu den Wurzelrippen steht, noch die Profiltiefen der einzelnen Teilbereiche die gleiche Tiefe aufweisen.