 |
 |
| Aus der Flugpraxis entwickelte theoretische Abhandlungen über: |
 |
|
|
 |
|
|
 |
|
|
 |
 |
|
|
 |
|
|
In dem Beitrag 'Die verflixte Luftschraubenanpassung' wurde die Problematik Antrieb und Luftschraubengröße bei Verwendung handelsüblicher Propeller, wenn auch sehr vereinfacht, doch recht ausführlich dargestellt. Etwas schmökern darin, könnte für nachfolgende Lektüre dem einen oder anderen Leser von Nutzen sein.
Abmessungen von BLATTBREITE und STEIGUNG egal?
Bei der Propellerwahl wird meistens das Hauptaugenmerk auf den Durchmesser gerichtet, schon weniger auf die Steigung und fast gar nicht auf die Blatttiefe. Aus einem Praxisbeispiel wird ersichtlich, warum die in der Überschrift genannten Luftschraubenparameter sehr wohl und wann zu beachten sind.
|
Beispiel: eine erst kürzlich vorgenommene Standmessung eines einfachen E-Antriebes bei exakt gleicher Spannung erbrachte ein unerwartetes Resultat. Die Stromaufnahme der kleine-ren 11 x 8,347* Luftschraube war beträchtlich größer als jene der größeren 12 x 5,996* aus gleicher Blattpalette (Grundriss) einer Firma! (* = beide Steigungen wurden an der Blattprofil-tangente bei r 0,7 nachgemessen).
Zur weiteren Behandlung dieses Beispiels scheint zunächst eine vereinfachte grafische Darstellung der Propellerblattwinkel hilfreich. In Abbildung 1 und 2-5 sind:
|
 |
v = die Fluggeschwindigkeit des Modells mit Antrieb (m/s) |
 |
vR, r = die Umfangs- auch Blattwinkelgeschwindigkeit (m/s), für die Textbeispiele ist r = 0,7! |
 |
vres, r = die resultierende Blattanströmgeschwindigkeit aus v, vi und vR. r (m/s) |
 |
αr = (Alpha) der aerodynamische Anstellwinkel [Dimension für alle Winkel (°)] |
 |
αi, r = der induzierte Anströmwinkel |
 |
βr = (Beta) der messbare Blattwinkel (Winkel der Blattsteigung) |
 |
Χr = (Chi) der aus v und vR. r = vres. r resultierende Fortschritts- oder Helixwinkel (Helix = schraubenförmig gewunden) |
 |
Φr = (Phi) der aerodynamische Anströmwinkel (aus Χr und αi, r) |
 |
tr = Blattprofiltiefe (m), D = Durchmesser (m), R = Radius (m), r = Radiusstation (%) |
| Zu den Bezeichnungen: tiefer gesetzte Buchstaben sind Indizes. Z.B. ist bei vR, r, R der Index für Rotation und r der für eine gewählte Radiusstation. |
|
|
|
Die Abb. 2 - 5 zeigen ein steigungsfestes Propellerprofil an einer x-beliebigen Radiusstelle r bei konstanter Drehzahl n aber zunehmender Fluggeschwindigkeit v und die sich dadurch verändernden Anstellwinkel αr der Luftschraube. Der besseren Übersicht wegen, ohne den induzierten Anströmwinkel αi, r. |
|
|
Abb. 2: im Standlauf ist die Fluggeschwindigkeit v = 0 und nur die Umdrehungsgeschwindigkeit vR.r wirksam. Hier ist also der Anstellwinkel αr am größten, weil der Anströmwinkel Χr = 0 ist. Folglich erzeugt die Luftschraube auch den größten Schub (Standschub: αr = βr).
Abb. 3: mit beginnender, zunehmender Fluggeschwindigkeit v wird, bis vres, r in einem entsprechenden Verhältnis zum Steigungswinkel steht, der optimale Anstellwinkel αr und damit auch die günstigste Anströmung am Propellerblatt erreicht.
|
Die Größe des aerodynamischen Winkels αr ist auch blattprofilabhängig. Bei symmetrischen Blattprofilen sollte er je nach Modelltyp klein sein, etwa 0,5 - 1°, bei konkaven Profilen bis 3,5°. Unter Berücksichtigung dessen ergibt sich bei Verwendung verschiedener Profile im Propellerblatt schon eine recht praktische Blattwinkelverteilung!
|
Abb. 4: die resultierende Blattgeschwindigkeit vres, r hat nun eine Größe erreicht, bei der αr = 0° ist. Hier dreht die Luftschraube leer durch und es wird kein Schub mehr erzeugt.
Abb. 5: wird v noch mehr gesteigert, wird αr negativ und die Luftschraube wird wie eine Freilaufschraube vom Fahrtwind durchgedreht (auch als Windmühleneffekt bekannt). Der Schub wirkt in umgekehrter Richtung und bremst den Flug. Dieser Zustand stellt sich auch beim Gleitflug mit Leerlauf bei kleinen vR, r und Drehzahlen n ein. |
Abhandlung des Beispiels:
Zunächst sollte man die Formel zur Berechnung der Antriebsleistung der von der Luftschraube beanspruchten Motorausgangsleistung Pw im Standbetrieb beachten: Pw = D5 * ρ * cp * (n/60)³ mit Durchmesser D (m), Luftwert ρ (Rho) ~ 1,206 kg/m³, Leistungsbeiwert cp (-), Drehzahl n (U/min). Wie ersichtlich, geht in ihr der Durchmesser D der Luftschraube mit der 5. Potenz ein und die Drehzahl zur 3. Potenz. Nicht aber die Steigung, wie in manchen Veröffentlichungen fälschlicherweise angegeben wird. Sie versteckt sich allenfalls in dem Leistungsbeiwert cp. Im Beispielfall erreicht cp Werte von 0,042 für die kleine und 0,06 für die größere Steigung (cp-Werte lassen sich aus dem Leistungs-Geschwindigkeitskoeffizienten cs und dem Fortschrittsgrad λ errechnen: cp = (λ/cs)5. Für beide Luftschrauben wurde bei gleicher Spannung (V) zunächst die Drehzahl ermittelt und dann Pw nach obiger Gleichung errechnet. Demnach sollte die kleinere Luftschraube 24,0 W Motorausgangsleistung beanspruchen, die größere hingegen 30,0 W
Dieses Ergebnis steht aber im völligen Widerspruch zu der eingangs erwähnten Standstrommessung, die schon aus reiner Neugierde vor dem Einbau in das Modell vorgenommen wurde. Befriedigt festgestellt wurde dabei zunächst eine optimale Stromaufnahme Iopt ( 'Die geheimnisvolle Tarnkappe 400'). Im Vertrauen darauf, dass der Antrieb als erprobt anzusehen war, konnte nun wirklich nicht vorausgesehen werden, dass dieser optimal erscheinende Stromaufnahmewert nur auf Grund eines abgerissen arbeitenden Propellerblattes (hoher Widerstand) zustande kam. Da dann aber auch im Flug die Steigleistung mehr als miserabel war - die gegenüber der Standmessung einsetzende Fluggeschwindigkeit v konnte resultierend den Anströmwinkel Χ nicht genügend vergrößern - wurde als ziemlich sicher konstatiert, dass bei dem schmalen Luftschraubenblatt und dem zu großen Anstellwinkel α, sich die Blattströmung in einem abgerissenen Strömungszustand befand.
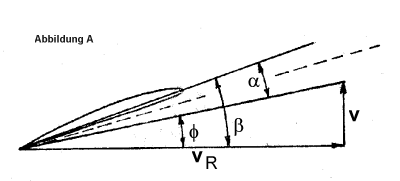
Die maßstabgerechte Abbildung A stellt nicht nur die Blattwinkelverhältnisse der empfohlenen! 11 x 8,347 Luftschraube dar (H/D = 0,76), sondern bestätigt auch die obige Annahme. Bei einem Blattwinkel β0,7 = 19° beträgt der Winkel α (ohne αi) 8,13°! Die gestrichelte Linie zeigt dagegen den idealen Winkel der Blattsteigung bei r0,7 zur gegenständlichen Flug- und Umfangsgeschwindigkeit.
Daraus kann man aber auch eine gewisse Selbstregelung der Luftschraubensteigung bei Starrluftschrauben ableiten, falls deren Propellerleistung nicht zu einem senkrechten Steigflug befähigt. Wird z.B. bei so einem Modell der Steigflugwinkel so lange gesteigert bis v gleich Null wird, ist der Anstellwinkel gleich dem Blattsteigungswinkel. Dann wird die gesamte Propellerenergie dazu benützt, lediglich das Gewicht des Modells, ohne Vorwärtsbewegung zu heben. Wird dagegen der Steigflugwinkel verkleinert, erhöht sich die Fluggeschwindigkeit, der Anstellwinkel wird kleiner und erreicht irgendwo sein Optimum. Das heißt, dass bei einer nicht zu großen Fehlanpassung der Steigung, sich diese in etwa durch den Steigflugwinkel mehr oder weniger selbst reguliert. Der optimale Steigflugwinkel, gegeben durch einen konstruktiv richtigen Blattwinkel β, wird dann aber nicht erreicht.
|
 |
Langsame Bahnfluggeschwindigkeit v, und eine verhältnismäßig kleine Umfangsgeschwindigkeit vR, 0,7, bedingt durch den schwachen, 4:1 untersetzten Antrieb, ergeben einen kleinen Anströmwinkel Χ 0,7. Dadurch entsteht gegenüber dem sehr großen Blattwinkel β0,7 ein viel zu großer Anstellwinkel α0,7.
Hinzu kommt noch die geringe Tiefe des leistungsbringenden Blattbereiches. Unter solchen Voraussetzungen wird die kritische Re-Zahl sicher unterschritten.
Erst mit einer Luftschraube größeren Durchmessers, demzufolge einer 18,6% größeren Blatttiefe und kleinerer Steigung (H/D = 0,5), also kleinerem Blattwinkel β0,7 (siehe tieferstehendes Kästchen), konnte der Punkt der kritischen Re-Zahl überwunden werden. Jetzt würde α0,7 nurmehr 3,42° betragen. Zieht man jedoch noch αi ab, wird der aerodynamische Anstellwinkel α0,7 schon recht klein und damit der Schub zu gering!
|
| Bei konstanter Steigung H verkleinert sich der Steigungswinkel β0,7 mit zunehmendem Durchmesser D! |
| D / H (") |
9 x 6 |
10 x 6 |
11 x 6 |
12 x 6 |
| D / H (m) |
230 / 150 |
250 / 150 |
280 / 150 |
300 / 150 |
| β0,7 (°) |
16,51 |
15,26 |
13,69 |
12,80 |
|
|
Wie erwartet, verringerte sich der Stromverbrauch beim zunächst empfohlenen Antrieb 1719, trotz größerer Luftschraube (siehe unterlegten Kasten) und gestiegener Drehzahl beträchtlich. Der nächste, besser geeignete Antrieb 1718 nimmt mit der größeren 12 x 6 Luftschraube bei sechs Zellen ideale 4,6 A auf. Leider ist auch hier die Steigung nach wie vor zu klein. Eine Erhöhung des Steigungswinkels bei r = 0,7 von 13° auf 15°, was dann einer Steigung von 6,95" oder 0,176 m entspräche (H/D = 0,58), würde schließlich auch diese Fehlanpassung beheben. Die Strombelastung sollte sich dann mit dieser 12x7 Luftschraube um 6,5 A bewegen.
Zur Wiederholung und zum merken:
- Bei Erhöhung der Motordrehzahl n, also Vergrößerung der Propeller-Rotationsgeschwindigkeit vR , wird der Winkel Φ kleiner, dadurch der Anstellwinkel α größer.
- Bei Verringerung der Motordrehzahl n, also Verkleinerung von vR , wird der Winkel Φ größer, dadurch der Anstellwinkel α kleiner.
- Mit zunehmender Fluggeschwindigkeit v wird der Winkel Φ größer, daher der Anstellwinkel α kleiner.
- Mit abnehmender Fluggeschwindigkeit v wird der Winkel Φ kleiner, daher der Anstellwinkel α größer.
Langsame Flugmodelle (Steigflug) mit stark untersetzten Antrieben, also kleinen Propellerdrehzahlen, verlangen - Durchmesser abhängig - kleine messbare Blattanstellwinkel, (Steigungen), somit kleinere H/D-Verhältnisse, betteln aber auch wegen der Gefahr des kritischen Re-Zahlbereiches unbedingt um größere Blattprofiltiefen. Im besten Wirkungsbereich sollten sie mit Profilen guter Profilgleitzahl ausgestattet sein.
Mit abgerissener Blattströmung arbeitende Luftschrauben sind laut (Hummeln)! Gut arbeitende Propeller hören sich verhältnismäßig leise an!
In einer weiteren Folge wird Ing. Rudolf Höbinger einen eleganten Weg zeigen, wie mittels Diagrammen schnell herausgefunden werden kann, ob der Blattsteigungswinkel β einer schon im Einsatz befindlichen Luftschraube richtig angepasst ist, oder ob Handlungsbedarf besteht.
|
|
 |

